# 数据结构进阶 @@ ## 目录 - 线段树 - 基本实现 - 线段树合并 - 线段树分裂 - 猫树 - 李超线段树 - $\mathrm{RMQ}$ - 单调栈 - $\mathrm{ST}$ 表 - 线段树 - $\mathrm{Four \ Russian}$ - 加减 $1$ $\mathrm{RMQ}$ @@ - 扫描线 - $\mathrm{Atlantis}$ 问题 - $\mathrm{B}$ 维正交范围 - 并查集应用 --- # 线段树 @@ ## 概念 线段树是算法竞赛中常用的用来维护 **区间信息** 的数据结构。 线段树可以在 $O(\log N)$ 的时间复杂度内实现单点修改、区间修改、区间查询（区间求和，求区间最大值，求区间最小值）等操作。 @@ ## 实现 ### 线段树的基本结构与建树 线段树将每个长度不为 $1$ 的区间划分成左右两个区间递归求解，把整个线段划分为一个树形结构，通过合并左右两区间信息来求得该区间的信息。这种数据结构可以方便的进行大部分的区间操作。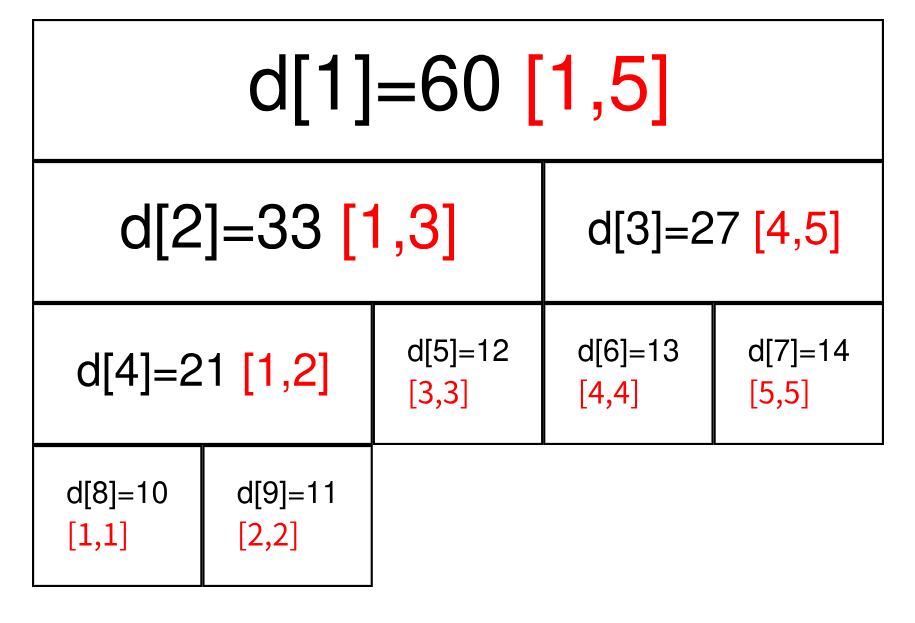 有个大小为 $5$ 的数组 $a=\{10,11,12,13,14\}$，要将其转化为线段树，有以下做法：设线段树的根节点编号为 $1$，用数组 $d$ 来保存我们的线段树，$d_i$ 用来保存线段树上编号为 $i$ 的节点的值（这里每个节点所维护的值就是这个节点所表示的区间总和）。 我们先给出这棵线段树的形态，如图所示： @@  @@ 图中每个节点中用红色字体标明的区间，表示该节点管辖的 $a$ 数组上的位置区间。如 $d_1$ 所管辖的区间就是 $[1,5]（a_1,a_2, \cdots ,a_5）$，即 $d_1$ 所保存的值是 $a_1+a_2+ \cdots +a_5$，$d_1=60$ 表示的是 $a_1+a_2+ \cdots +a_5=60$。 通过观察不难发现，$d_i$ 的左儿子节点就是 $d_{2\times i}$，$d_i$ 的右儿子节点就是 $d_{2\times i+1}$。如果 $d_i$ 表示的是区间 $[s,t]$（即 $d_i=a_s+a_{s+1}+ \cdots +a_t$）的话，那么 $d_i$ 的左儿子节点表示的是区间 $[ s, \frac{s+t}{2} ]$，$d_i$ 的右儿子表示的是区间 $[ \frac{s+t}{2} +1,t ]$。 在实现时，我们考虑递归建树。设当前的根节点为 $p$，如果根节点管辖的区间长度已经是 $1$，则可以直接根据 $a$ 数组上相应位置的值初始化该节点。否则我们将该区间从中点处分割为两个子区间，分别进入左右子节点递归建树，最后合并两个子节点的信息。 @@ 代码实现： ```cpp void build(int s, int t, int p) { // 对 [s,t] 区间建立线段树,当前根的编号为 p if (s == t) { d[p] = a[s]; return; } int m = s + ((t - s) >> 1); // 移位运算符的优先级小于加减法，所以加上括号 // 如果写成 (s + t) >> 1 可能会超出 int 范围 build(s, m, p * 2), build(m + 1, t, p * 2 + 1); // 递归对左右区间建树 d[p] = d[p * 2] + d[(p * 2) + 1]; } ``` @@ 关于线段树的空间：如果采用堆式存储（$2p$ 是 $p$ 的左儿子，$2p+1$ 是 $p$ 的右儿子），若有 $n$ 个叶子结点，则 $d$ 数组的范围最大为 $2^{\left\lceil\log{n}\right\rceil+1}$。 分析：容易知道线段树的深度是 $\left\lceil\log{n}\right\rceil$ 的，则在堆式储存情况下叶子节点（包括无用的叶子节点）数量为 $2^{\left\lceil\log{n}\right\rceil}$ 个，又由于其为一棵完全二叉树，则其总节点个数 $2^{\left\lceil\log{n}\right\rceil+1}-1$。当然如果你懒得计算的话可以直接把数组长度设为 $4n$，因为 $\frac{2^{\left\lceil\log{n}\right\rceil+1}-1}{n}$ 的最大值在 $n=2^{x}+1(x\in N_{+})$ 时取到，此时节点数为 $2^{\left\lceil\log{n}\right\rceil+1}-1=2^{x+2}-1=4n-5$。 @@ ### 线段树的区间查询 区间查询，比如求区间 $[l,r]$ 的总和（即 $a_l+a_{l+1}+ \cdots +a_r$）、求区间最大值/最小值等操作。  仍然以最开始的图为例，如果要查询区间 $[1,5]$ 的和，那直接获取 $d_1$ 的值（$60$）即可。 如果要查询的区间为 $[3,5]$，此时就不能直接获取区间的值，但是 $[3,5]$ 可以拆成 $[3,3]$ 和 $[4,5]$，可以通过合并这两个区间的答案来求得这个区间的答案。 一般地，如果要查询的区间是 $[l,r]$，则可以将其拆成最多为 $O(\log n)$ 个 极大 的区间，合并这些区间即可求出 $[l,r]$ 的答案。 @@ 代码实现： ```cpp int getsum(int l, int r, int s, int t, int p) { // [l, r] 为查询区间, [s, t] 为当前节点包含的区间, p 为当前节点的编号 if (l <= s && t <= r) return d[p]; // 当前区间为询问区间的子集时直接返回当前区间的和 int m = s + ((t - s) >> 1), sum = 0; if (l <= m) sum += getsum(l, r, s, m, p * 2); // 如果左儿子代表的区间 [s, m] 与询问区间有交集, 则递归查询左儿子 if (r > m) sum += getsum(l, r, m + 1, t, p * 2 + 1); // 如果右儿子代表的区间 [m + 1, t] 与询问区间有交集, 则递归查询右儿子 return sum; } ``` @@ ### 线段树的区间修改与懒惰标记 如果要求修改区间 $[l,r]$，把所有包含在区间 $[l,r]$ 中的节点都遍历一次、修改一次，时间复杂度无法承受。我们这里要引入一个叫做 **「懒惰标记」** 的东西。 懒惰标记，简单来说，就是通过延迟对节点信息的更改，从而减少可能不必要的操作次数。每次执行修改时，我们通过打标记的方法表明该节点对应的区间在某一次操作中被更改，但不更新该节点的子节点的信息。实质性的修改则在下一次访问带有标记的节点时才进行。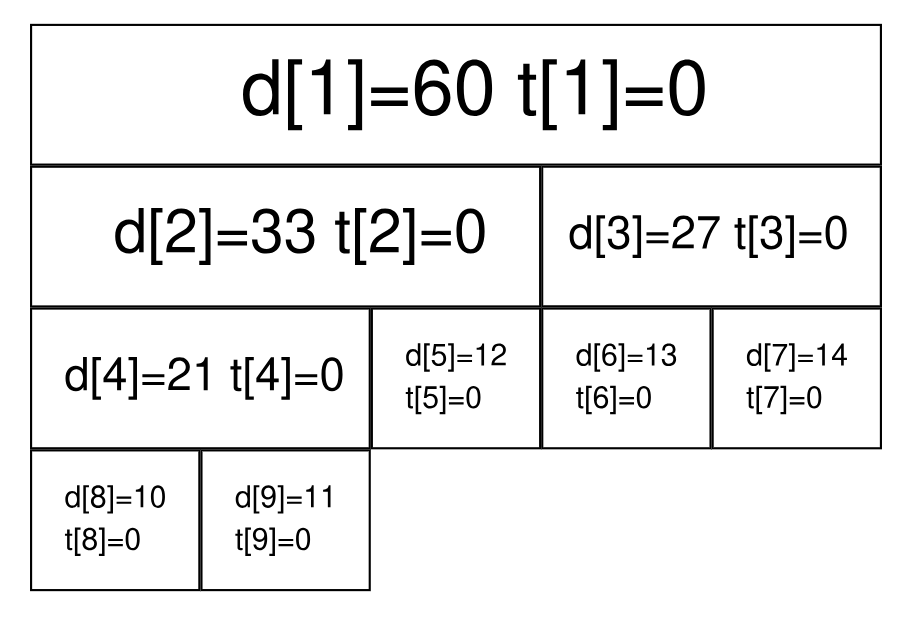 仍然以最开始的图为例，我们将执行若干次给区间内的数加上一个值的操作。我们现在给每个节点增加一个 $t_i$，表示该节点带的标记值。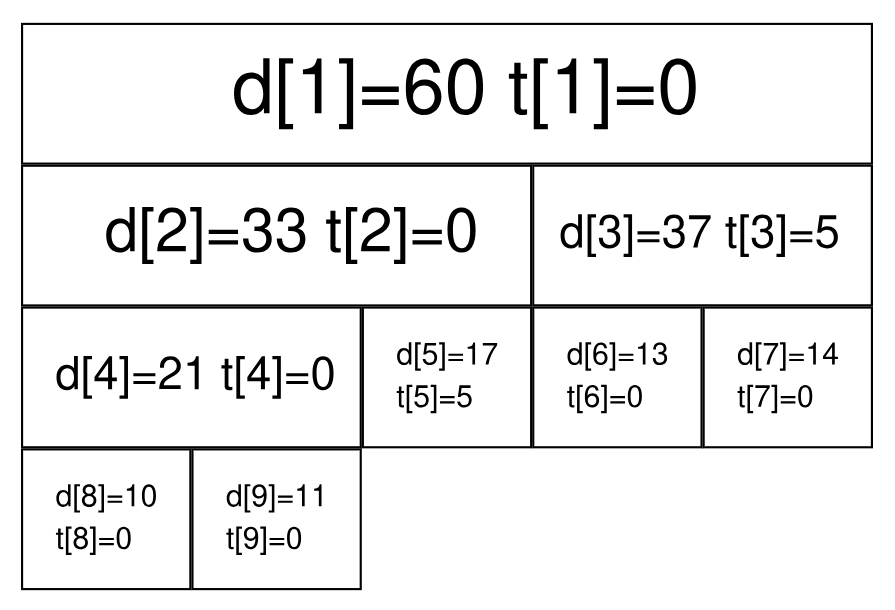 @@ 最开始时的情况是这样的：  @@ 现在我们准备给 $[3,5]$ 上的每个数都加上 $5$。根据前面区间查询的经验，我们很快找到了两个极大区间 $[3,3]$ 和 $[4,5]$（分别对应线段树上的 $3$ 号点和 $5$ 号点）。 我们直接在这两个节点上进行修改，并给它们打上标记：  @@ 我们发现，$3$ 号节点的信息虽然被修改了（因为该区间管辖两个数，所以 $d_3$ 加上的数是 $5 \times 2=10$），但它的两个子节点却还没更新，仍然保留着修改之前的信息。不过不用担心，虽然修改目前还没进行，但当我们要查询这两个子节点的信息时，我们会利用标记修改这两个子节点的信息，使查询的结果依旧准确。 接下来我们查询一下 $[4,4]$ 区间上各数字的和。 我们通过递归找到 $[4,5]$ 区间，发现该区间并非我们的目标区间，且该区间上还存在标记。这时候就到标记下放的时间了。我们将该区间的两个子区间的信息更新，并清除该区间上的标记。 @@  现在 $6$、$7$ 两个节点的值变成了最新的值，查询的结果也是准确的。 @@ 接下来给出在存在标记的情况下，区间修改和查询操作的参考实现。 代码实现： ```cpp void update(int l, int r, int c, int s, int t, int p) { // [l, r] 为修改区间, c 为被修改的元素的变化量, [s, t] 为当前节点包含的区间, p // 为当前节点的编号 if (l <= s && t <= r) { d[p] += (t - s + 1) * c, b[p] += c; return; } // 当前区间为修改区间的子集时直接修改当前节点的值,然后打标记,结束修改 int m = s + ((t - s) >> 1); if (b[p] && s != t) { // 如果当前节点的懒标记非空,则更新当前节点两个子节点的值和懒标记值 d[p * 2] += b[p] * (m - s + 1), d[p * 2 + 1] += b[p] * (t - m); b[p * 2] += b[p], b[p * 2 + 1] += b[p]; // 将标记下传给子节点 b[p] = 0; // 清空当前节点的标记 } if (l <= m) update(l, r, c, s, m, p * 2); if (r > m) update(l, r, c, m + 1, t, p * 2 + 1); d[p] = d[p * 2] + d[p * 2 + 1]; } ``` @@ ```cpp int getsum(int l, int r, int s, int t, int p) { // [l, r] 为查询区间, [s, t] 为当前节点包含的区间, p 为当前节点的编号 if (l <= s && t <= r) return d[p]; // 当前区间为询问区间的子集时直接返回当前区间的和 int m = s + ((t - s) >> 1); if (b[p]) { // 如果当前节点的懒标记非空,则更新当前节点两个子节点的值和懒标记值 d[p * 2] += b[p] * (m - s + 1), d[p * 2 + 1] += b[p] * (t - m); b[p * 2] += b[p], b[p * 2 + 1] += b[p]; // 将标记下传给子节点 b[p] = 0; // 清空当前节点的标记 } int sum = 0; if (l <= m) sum = getsum(l, r, s, m, p * 2); if (r > m) sum += getsum(l, r, m + 1, t, p * 2 + 1); return sum; } ``` @@ ### 动态开点线段树 前面讲到堆式储存的情况下，需要给线段树开 $4n$ 大小的数组。为了节省空间，我们可以不一次性建好树，而是在最初只建立一个根结点代表整个区间。当我们需要访问某个子区间时，才建立代表这个区间的子结点。这样我们不再使用 $2p$ 和 $2p+1$ 代表 $p$ 结点的儿子，而是用 $\text{ls}$ 和 $\text{rs}$ 记录儿子的编号。总之，动态开点线段树的核心思想就是：结点只有在有需要的时候才被创建。 单次操作的时间复杂度是不变的，为 $O(\log n)$。由于每次操作都有可能创建并访问全新的一系列结点，因此 $m$ 次单点操作后结点的数量规模是 $O(m\log n)$。最多也只需要 $2n-1$ 个结点，没有浪费。 @@ 单点修改： ```cpp // root 表示整棵线段树的根结点；cnt 表示当前结点个数 int n, cnt, root; int sum[n * 2], ls[n * 2], rs[n * 2]; // 用法：update(root, 1, n, x, f); 其中 x 为待修改节点的编号 void update(int& p, int s, int t, int x, int f) { // 引用传参 if (!p) p = ++cnt; // 当结点为空时，创建一个新的结点 if (s == t) { sum[p] += f; return; } int m = s + ((t - s) >> 1); if (x <= m) update(ls[p], s, m, x, f); else update(rs[p], m + 1, t, x, f); sum[p] = sum[ls[p]] + sum[rs[p]]; // pushup } ``` @@ 区间查询： ```cpp // 用法：query(root, 1, n, l, r); int query(int p, int s, int t, int l, int r) { if (!p) return 0; // 如果结点为空，返回 0 if (s >= l && t <= r) return sum[p]; int m = s + ((t - s) >> 1), ans = 0; if (l <= m) ans += query(ls[p], s, m, l, r); if (r > m) ans += query(rs[p], m + 1, t, l, r); return ans; } ``` 区间修改也是一样的，不过下放标记时要注意如果缺少孩子，就直接创建一个新的孩子。或者使用标记永久化技巧。 @@ ### 一些优化 这里总结几个线段树的优化： 在叶子节点处无需下放懒惰标记，所以懒惰标记可以不下传到叶子节点。 下放懒惰标记可以写一个专门的函数 ```pushdown```，从儿子节点更新当前节点也可以写一个专门的函数 ```maintain```（或者对称地用 ```pushup```），降低代码编写难度。 标记永久化：如果确定懒惰标记不会在中途被加到溢出（即超过了该类型数据所能表示的最大范围），那么就可以将标记永久化。标记永久化可以避免下传懒惰标记，只需在进行询问时把标记的影响加到答案当中，从而降低程序常数。具体如何处理与题目特性相关，需结合题目来写。这也是树套树和可持久化数据结构中会用到的一种技巧。 @@ ## 线段树合并 顾名思义，线段树合并是指建立一棵新的线段树，这棵线段树的每个节点都是两棵原线段树对应节点合并后的结果。它常常被用于维护树上或是图上的信息。 显然，我们不可能真的每次建满一颗新的线段树，因此我们需要使用上文的动态开点线段树。 线段树合并的过程本质上相当暴力： 假设两颗线段树为 $A$ 和 $B$，我们从 $1$ 号节点开始递归合并。 递归到某个节点时，如果 $A$ 树或者 $B$ 树上的对应节点为空，直接返回另一个树上对应节点，这里运用了动态开点线段树的特性。 如果递归到叶子节点，我们合并两棵树上的对应节点。 最后，根据子节点更新当前节点并且返回。 @@ 代码实现： ```cpp int merge(int a, int b, int l, int r) { if (!a) return b; if (!b) return a; if (l == r) { // do something... return a; } int mid = (l + r) >> 1; tr[a].l = merge(tr[a].l, tr[b].l, l, mid); tr[a].r = merge(tr[a].r, tr[b].r, mid + 1, r); pushup(a); return a; } ``` @@ ### 例题 [P4556 [Vani有约会] 雨天的尾巴 /【模板】线段树合并](https://www.luogu.com.cn/problem/P4556) 题目描述： - 首先村落里的一共有 $n$ 座房屋，并形成一个树状结构。然后救济粮分 $m$ 次发放，每次选择两个房屋 $(x,y)$，然后对于 $x$ 到 $y$ 的路径上（含 $x$ 和 $y$）每座房子里发放一袋 $z$ 类型的救济粮。 - 然后深绘里想知道，当所有的救济粮发放完毕后，每座房子里存放的最多的是哪种救济粮。 @@ 思路： 线段树分裂模板题，将 $[x,y]$ 分裂出来。 - 将 $t$ 树合并入 $p$ 树：单次合并即可。 - $p$ 树中插入 $x$ 个 $q$：单点修改。 - 查询 $[x,y]$ 中数的个数：区间求和。 - 查询第 $k$ 小。 @@ ## 线段树分裂 线段树分裂实质上是线段树合并的逆过程。线段树分裂只适用于有序的序列，无序的序列是没有意义的，常用在动态开点的权值线段树。 注意当分裂和合并都存在时，我们在合并的时候必须回收节点，以避免分裂时会可能出现节点重复占用的问题。 从一颗区间为 $[1,N]$ 的线段树中分裂出 $[l,r]$，建一颗新的树： 从 $1$ 号结点开始递归分裂，当节点不存在或者代表的区间 $[s,t]$ 与 $[l,r]$ 没有交集时直接回溯。 当 $[s,t]$ 与 $[l,r]$ 有交集时需要开一个新结点。 当 $[s,t]$ 包含于 $[l,r]$ 时，需要将当前结点直接接到新的树下面，并把旧边断开。 @@ 代码实现： ```cpp void split(int &p, int &q, int s, int t, int l, int r) { if (t < l || r < s) return; if (!p) return; if (l <= s && t <= r) { q = p; p = 0; return; } if (!q) q = New(); int m = s + t >> 1; if (l <= m) split(ls[p], ls[q], s, m, l, r); if (m < r) split(rs[p], rs[q], m + 1, t, l, r); push_up(p); push_up(q); } ``` @@ ### 例题 [P5494【模板】线段树分裂](https://www.luogu.com.cn/problem/P5494) 题目描述： 给出一个可重集 $a$（编号为 $1$），它支持以下操作： - $0 \ p \ x \ y$：将可重集 $p$ 中大于等于 $x$ 且小于等于 $y$ 的值移动到一个新的可重集中（新可重集编号为从 $2$ 开始的正整数，是上一次产生的新可重集的编号$+1$）。 - $1 \ p \ t$：将可重集 $t$ 中的数放入可重集 $p$，且清空可重集 $t$（数据保证在此后的操作中不会出现可重集 $t$）。 - $2 \ p \ x \ q$：在 $p$ 这个可重集中加入 $x$ 个数字 $q$。 - $3 \ p \ x \ y$：查询可重集 $p$ 中大于等于 $x$ 且小于等于 $y$ 的值的个数。 - $4 \ p \ k$：查询在 $p$ 这个可重集中第 $k$ 小的数，不存在时输出 $-1$。 @@ 思路： 线段树分裂模板题，将 $[x,y]$ 分裂出来。 - 将 $t$ 树合并入 $p$ 树：单次合并即可。 - $p$ 树中插入 $x$ 个 $q$：单点修改。 - 查询 $[x,y]$ 中数的个数：区间求和。 - 查询第 $k$ 小。 @@ ## 线段树优化建图 在建图连边的过程中，我们有时会碰到这种题目，一个点向一段连续的区间中的点连边或者一个连续的区间向一个点连边，如果我们真的一条一条连过去，那一旦点的数量多了复杂度就爆炸了，这里就需要用线段树的区间性质来优化我们的建图了。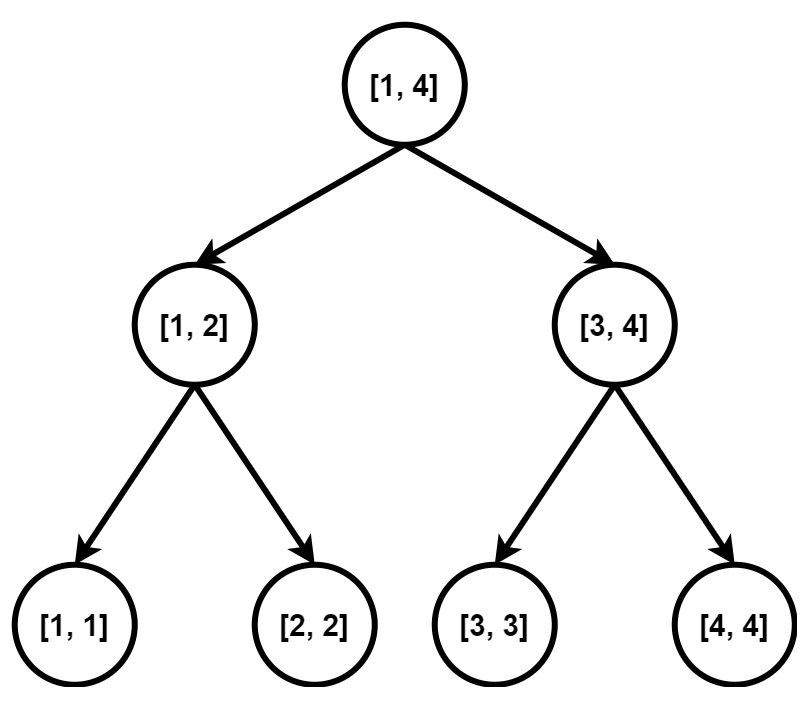 @@ 下面是一个线段树。  @@ 每个节点都代表了一个区间，假设我们要向区间 $[2, 4]$ 连边。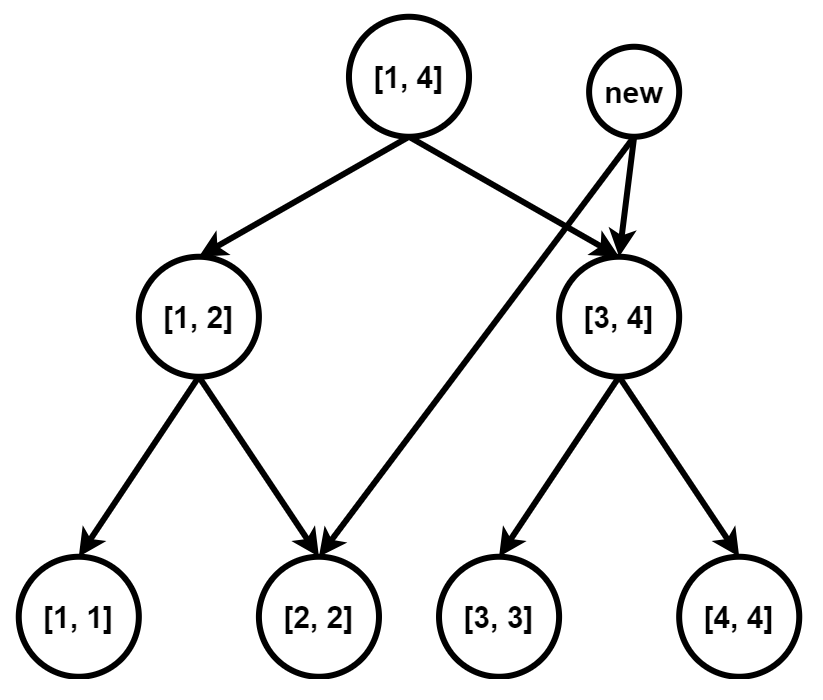  @@ 在一些题目中，还会出现一个区间连向一个点的情况，则我们将上面第一张图的有向边全部反过来即可，上面的树叫做入树，下面这个叫做出树。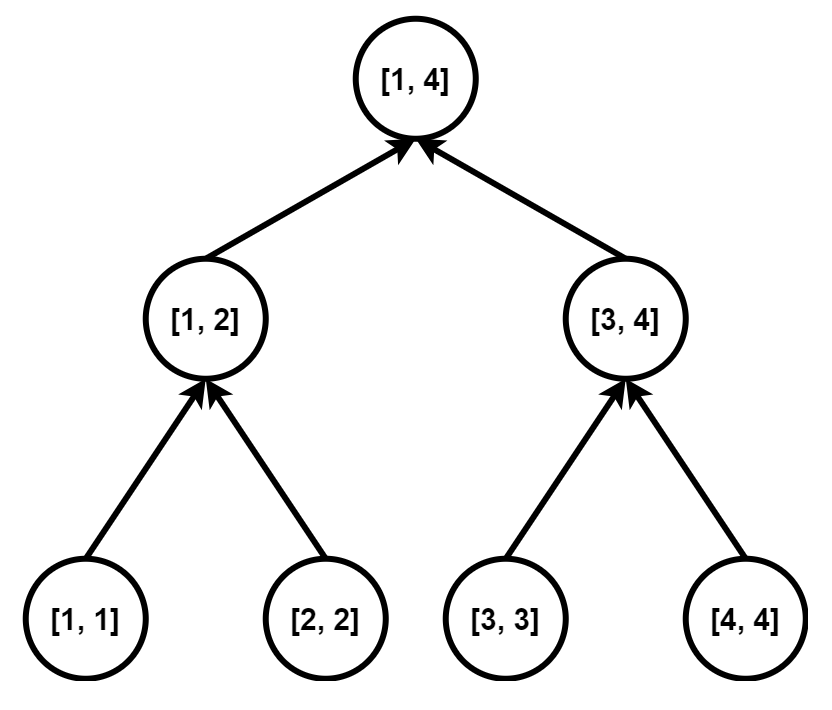  @@ ### 例题 [Legacy](https://codeforces.com/problemset/problem/786/B) 题目描述： 有 $n$ 个点、$q$ 次操作。每一种操作为以下三种类型中的一种： - 操作一：连一条 $u \rightarrow v$ 的有向边，权值为 $w$。 - 操作二：对于所有 $i \in [l,r]$ 连一条 $u \rightarrow i$ 的有向边，权值为 $w$。 - 操作三：对于所有 $i \in [l,r]$ 连一条 $i \rightarrow u$ 的有向边，权值为 $w$。 求从点 $s$ 到其他点的最短路，$(1 \le n,q \le 10^5, 1 \le w \le 10^9)$。 @@ ## 拓展 - 猫树 众所周知线段树可以支持高速查询某一段区间的信息和，比如区间最大子段和，区间和，区间矩阵的连乘积等等。 但是有一个问题在于普通线段树的区间询问在某些毒瘤的眼里可能还是有些慢了。 简单来说就是线段树建树的时候需要做 $O(n)$ 次合并操作，而每一次区间询问需要做 $O(\log{n})$ 次合并操作，询问区间和这种东西的时候还可以忍受，但是当我们需要询问区间线性基这种合并复杂度高达 $O(\log^2{w})$ 的信息的话，此时就算是做 $O(\log{n})$ 次合并有些时候在时间上也是不可接受的。 @@ 而所谓「猫树」就是一种不支持修改，仅仅支持快速区间询问的一种静态线段树。 构造一棵这样的静态线段树需要 $O(n\log{n})$ 次合并操作，但是此时的查询复杂度被加速至 $O(1)$ 次合并操作。 在处理线性基这样特殊的信息的时候甚至可以将复杂度降至 $O(n\log^2{w})$。 @@ ### 原理 在查询 $[l,r]$ 这段区间的信息和的时候，将线段树树上代表 $[l,l]$ 的节点和代表 $[r,r]$ 这段区间的节点在线段树上的 $\text{LCA}$ 求出来，设这个节点 $p$ 代表的区间为 $[L,R]$，我们会发现一些非常有趣的性质： - $[L,R]$ 这个区间一定包含 $[l,r]$。显然，因为它既是 $l$ 的祖先又是 $r$ 的祖先。 - $[l,r]$ 这个区间一定跨越 $[L,R]$ 的中点。由于 $p$ 是 $l$ 和 $r$ 的 $\text{LCA}$，这意味着 $p$ 的左儿子是 $l$ 的祖先而不是 $r$ 的祖先，$p$ 的右儿子是 $r$ 的祖先而不是 $l$ 的祖先。因此，$l$ 一定在 $[L,\mathit{mid}]$ 这个区间内，$r$ 一定在 $(\mathit{mid},R]$ 这个区间内。 有了这两个性质，我们就可以将询问的复杂度降至 $O(1)$ 了。 @@ ### 实现 具体来讲我们建树的时候对于线段树树上的一个节点，设它代表的区间为 $(l,r]$。 不同于传统线段树在这个节点里只保留 $[l,r]$ 的和，我们在这个节点里面额外保存 $(l,\mathit{mid}]$ 的后缀和数组和 $(\mathit{mid},r]$ 的前缀和数组。 这样的话建树的复杂度为 $T(n)=2T(n/2)+O(n)=O(n\log{n})$ 同理空间复杂度也从原来的 $O(n)$ 变成了 $O(n\log{n})$。 @@ 下面是最关键的询问了。 如果我们询问的区间是 $[l,r]$ 那么我们把代表 $[l,l]$ 的节点和代表 $[r,r]$ 的节点的 $\text{LCA}$ 求出来，记为 $p$。 根据刚才的两个性质，$l$,$r$ 在 $p$ 所包含的区间之内并且一定跨越了 $p$ 的中点。 这意味这一个非常关键的事实是我们可以使用 $p$ 里面的前缀和数组和后缀和数组，将 $[l,r]$ 拆成 $[l,\mathit{mid}]+(\mathit{mid},r]$ 从而拼出来 $[l,r]$ 这个区间。 而这个过程仅仅需要 $O(1)$ 次合并操作！ 不过我们好像忽略了点什么？ 似乎求 $\text{LCA}$ 的复杂度似乎还不是 $O(1)$，暴力求是 $O(\log{n})$ 的，倍增法则是 $O(\log{\log{n}})$ 的，转 ST 表的代价又太大…… @@ ### 堆式建树 具体来将我们将这个序列补成 $2$ 的整次幂，然后建线段树。 此时我们发现线段树上两个节点的 $\text{LCA}$ 编号，就是两个节点二进制编号的最长公共前缀 $\text{LCP}$。 稍作思考即可发现发现在 $x$ 和 $y$ 的二进制下 $lcp(x,y)=x>>log[x^y]$。 所以我们预处理一个 $log$ 数组即可轻松完成求 $LCA$ 的工作。 这样我们就构建了一个猫树。 由于建树的时候涉及到求前缀和和求后缀和，所以对于线性基这种虽然合并是 $O(\log^2{w})$ 但是求前缀和却是 $O(n\log{n})$ 的信息，使用猫树可以将静态区间线性基从 $O(n\log^2{w}+m\log^2{w}\log{n})$ 优化至 $O(n\log{n}\log{w}+m\log^2{w})$ 的复杂度。 @@ # RMQ问题 @@ ## 单调栈 详见单调栈 @@ ## ST表 详见ST表 @@ ## 线段树 详见线段树 @@ ## Four Russian $\text{Four russian}$ 是一个由四位俄罗斯籍的计算机科学家提出来的基于 $\text{ST}$ 表的算法。 在 $\text{ST}$ 表的基础上 $\text{Four russian}$ 算法对其做出的改进是序列分块。 具体来说，我们将原数组——我们将其称之为数组 $A$——每 $S$ 个分成一块，总共 $n/S$ 块。 对于每一块我们预处理出来块内元素的最小值，建立一个长度为 $n/S$ 的数组 $B$，并对数组 $B$ 采用 $\text{ST}$ 表的方式预处理。 同时，我们对于数组 $A$ 的每一个零散块也建立一个 $\text{ST}$ 表。 询问的时候，我们可以将询问区间划分为不超过 $1$ 个数组 $B$ 上的连续块区间和不超过 $2$ 个数组 $A$ 上的整块内的连续区间。显然这些问题我们通过 $\text{ST}$ 表上的区间查询解决。 @@ 在 $S=\log n$ 时候，预处理复杂度达到最优，为 $O((n / \log n)\log n+(n / \log n)\times\log n\times\log \log n)=O(n\log \log n)$。 时间复杂度 $O(n\log \log n) \sim O(1)$ 空间复杂度 $O(n\log \log n)$ 当然询问由于要跑三个 $\text{ST}$ 表，该实现方法的常数较大。 @@ ## 加减 1RMQ 若序列满足相邻两元素相差为 $1$，在这个序列上做 $\text{RMQ}$ 可以成为加减 $\text{1RMQ}$，根究这个特性可以改进 $\text{Four russian}$ 算法，做到 $O(n) \sim O(1)$ 的时间复杂度，$O(n)$ 的空间复杂度。 由于 $\text{Four russian}$ 算法的瓶颈在于块内 $\text{RMQ}$ 问题，我们重点去讨论块内 $\text{RMQ}$ 问题的优化。 由于相邻两个数字的差值为 $\pm 1$，所以在固定左端点数字时 长度不超过 $\log n$ 的右侧序列种类数为 $\sum_{i=1}^{\log n} 2^{i-1}$，而这个式子显然不超过 $n$。 这启示我们可以预处理所有不超过 $n$ 种情况的 最小值 $-$ 第一个元素 的值。 @@ 在预处理的时候我们需要去预处理同一块内相邻两个数字之间的差，并且使用二进制将其表示出来。 在询问的时候我们找到询问区间对应的二进制表示，查表得出答案。 这样子 $\text{Four russian}$ 预处理的时间复杂度就被优化到了 $O(n)$。 --- # 扫描线 @@ ## 概念 扫描线一般运用在图形上面，它和它的字面意思十分相似，就是一条线在整个图上扫来扫去，它一般被用来解决图形面积，周长，以及二维数点等问题。 @@ ## Atlantis 问题 在二维坐标系上，给出多个矩形的左下以及右上坐标，求出所有矩形构成的图形的面积。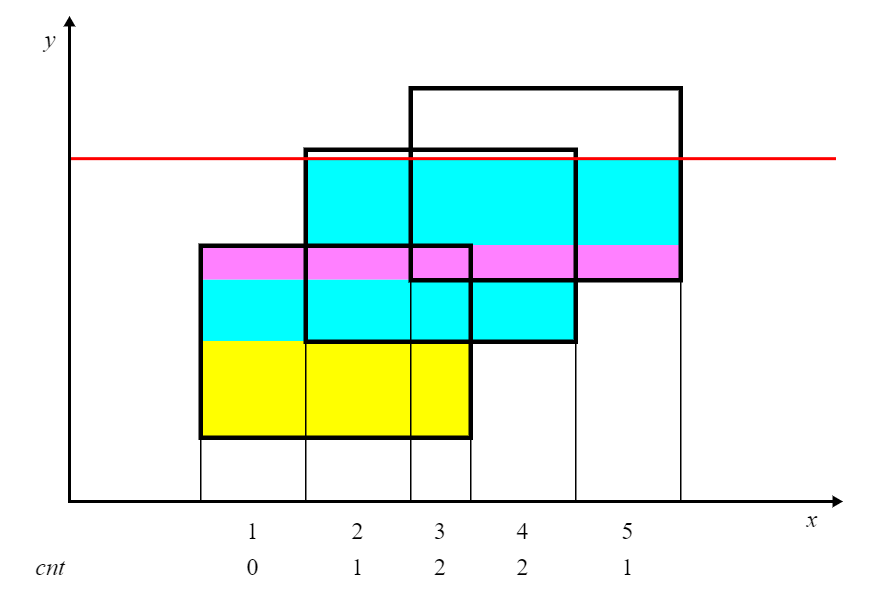 @@ ### 解法 现在假设我们有一根线，从下往上开始扫描：  - 如图所示，我们可以把整个矩形分成如图各个颜色不同的小矩形，那么这个小矩形的高就是我们扫过的距离，那么剩下了一个变量，那就是矩形的长一直在变化。 - 我们的线段树就是为了维护矩形的长，我们给每一个矩形的上下边进行标记，下面的边标记为 $1$，上面的边标记为 $-1$，每遇到一个矩形时，我们知道了标记为 $1$ 的边，我们就加进来这一条矩形的长，等到扫描到 $-1$ 时，证明这一条边需要删除，就删去，利用 $1$ 和 $-1$ 可以轻松的到这种状态。 - 还要注意这里的线段树指的并不是线段的一个端点，而指的是一个区间，所以我们要计算的是 $r+1$ 和 $r-1$。 - 需要离散化。 @@ ## B 维正交范围 $B$ 维正交范围指在一个 $B$ 维直角坐标系下，第 $i$ 维坐标在一个整数范围 $[l_i,r_i]$ 间，内部的点集。 一般来说，一维正交范围简称区间，二维正交范围简称矩形，三维正交范围简称立方体（我们常说的二维数点就是二维正交范围）。 对于一个静态的二维问题，我们可以使用扫描线扫一维，数据结构维护另一维。 在扫描线从左到右扫的过程中，会在数据结构维护的那一维上产生一些修改与查询。 如果查询的信息可差分的话直接使用差分，否则需要使用分治。差分一般用树状数组和线段树维护，但因为树状数组好写而且常数小，所以大部分人会选择用树状数组来维护。分治一般是 $\text{CDQ}$ 分治（但是这里不涉及分治）。 @@ 另一种比较容易理解的看待问题的角度是站在序列角度，而不站在二维平面角度。如果我们这样看待问题，则扫描线实际上是枚举了右端点 $r=1\cdots n$，维护一个数据结构，支持查询对于当前的 $r$，给定一个值 $l$，$l$ 到 $r$ 的答案是什么。即扫描线扫询问右端点，数据结构维护所有左端点的答案，或者说遍历一维，数据结果维护另一维。 复杂度一般为 $\mathcal O((n+m)\log n)$。 @@ ## 二维数点 给一个长为 $n$ 的序列，有 $m$ 次查询，每次查区间 $[l,r]$ 中值在 $[x,y]$ 内的元素个数。 这个问题就叫做二维数点。我们可以发现等价于我们要查询一个二维平面上矩形内的点的数量和。这里讲一下这个问题最简单的处理方法，扫描线 $+$ 树状数组。 很显然，这个问题是一个静态的二维问题，我们通过扫描线可以将静态的二维问题转换为动态的一维问题。维护动态的一维问题就使用数据结构维护序列，这里可以使用树状数组。 先将所有的询问离散化，用树状数组维护权值，对于每次询问的 $l$ 和 $r$，我们在枚举到 $l-1$ 时统计当前位于区间 $[x,y]$ 内的数的数量 $a$，继续向后枚举，枚举到 $r$ 时统计当前位于区间 $[x,y]$ 内的数的数量 $b$，$b-a$ 即为该次询问的答案。 --- # 并查集应用 @@ ## 内容 并查集，Kruskal 重构树的思维方式是很类似的，他们都能用于处理与连通性有关的问题。这里我们通过例题讲解的方式给大家介绍并查集思想的应用。 @@ ## Kruskal Kruskal 算法是一种常见并且好写的最小生成树算法，由 Kruskal 发明。该算法的基本思想是从小到大加入边，是个贪心算法。 @@ ### 实现  @@ 算法虽简单，但需要相应的数据结构来支持……具体来说，维护一个森林，查询两个结点是否在同一棵树中，连接两棵树。 抽象一点地说，维护一堆 **集合**，查询两个元素是否属于同一集合，合并两个集合。 其中，查询两点是否连通和连接两点可以使用并查集维护。 如果使用 $O(m\log m)$ 的排序算法，并且使用 $O(m\alpha(m, n))$ 或 $O(m\log n)$ 的并查集，就可以得到时间复杂度为 $O(m\log m)$ 的 $\text{Kruskal}$ 算法。 @@ ### 证明 思路很简单，为了造出一棵最小生成树，我们从最小边权的边开始，按边权从小到大依次加入，如果某次加边产生了环，就扔掉这条边，直到加入了 $n-1$ 条边，即形成了一棵树。 证明：使用归纳法，证明任何时候 $K$ 算法选择的边集都被某棵 $\text{MST}$ 所包含。 基础：对于算法刚开始时，显然成立（最小生成树存在）。 @@ 归纳：假设某时刻成立，当前边集为 $F$，令 $T$ 为这棵 $\text{MST}$，考虑下一条加入的边 $e$。 如果 $e$ 属于 $T$，那么成立。 否则，$T+e$ 一定存在一个环，考虑这个环上不属于 $F$ 的另一条边 $f$（一定只有一条）。 首先，$f$ 的权值一定不会比 $e$ 小，不然 $f$ 会在 $e$ 之前被选取。 然后，$f$ 的权值一定不会比 $e$ 大，不然 $T+e-f$ 就是一棵比 $T$ 还优的生成树了。 所以，$T+e-f$ 包含了 $F$，并且也是一棵最小生成树，归纳成立。 @@ ## Kruskal 重构树 在跑 $\text{Kruskal}$ 的过程中我们会从小到大加入若干条边。现在我们仍然按照这个顺序。 首先新建 $n$ 个集合，每个集合恰有一个节点，点权为 $0$。 每一次加边会合并两个集合，我们可以新建一个点，点权为加入边的边权，同时将两个集合的根节点分别设为新建点的左儿子和右儿子。然后我们将两个集合和新建点合并成一个集合。将新建点设为根。 不难发现，在进行 $n-1$ 轮之后我们得到了一棵恰有 $n$ 个叶子的二叉树，同时每个非叶子节点恰好有两个儿子。这棵树就叫 $\text{Kruskal}$ 重构树。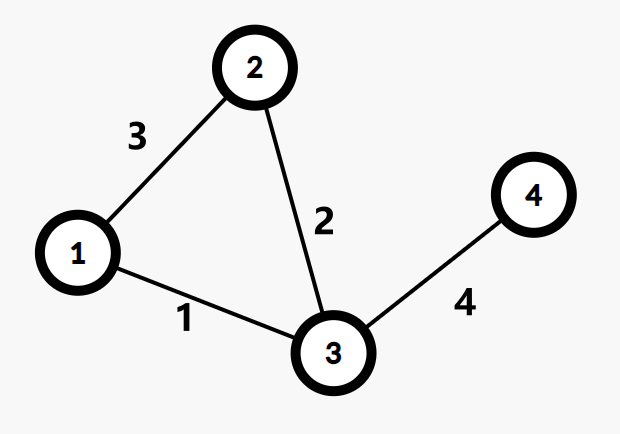 @@ 举个例子：  @@ 这张图的 Kruskal 重构树如下：  @@ ### 性质 不难发现，原图中两个点之间的所有简单路径上最大边权的最小值 $=$ 最小生成树上两个点之间的简单路径上的最大值 $= \text{Kruskal}$ 重构树上两点之间的 $\text{LCA}$ 的权值。 也就是说，到点 $x$ 的简单路径上最大边权的最小值 $\leq val$ 的所有点 $y$ 均在 $\text{Kruskal}$ 重构树上的某一棵子树内，且恰好为该子树的所有叶子节点。 我们在 $\text{Kruskal}$ 重构树上找到 $x$ 到根的路径上权值 $\leq val$ 的最浅的节点。显然这就是所有满足条件的节点所在的子树的根节点。 如果需要求原图中两个点之间的所有简单路径上最小边权的最大值，则在跑 $\text{Kruskal}$ 的过程中按边权大到小的顺序加边。 @@ ## 例题 ### $A$ 有 $n$ 个点，初始时均为孤立点。 接下来有 $m$ 次加边操作，第 $i$ 次操作在 $a_i$ 和 $b_i$ 之间加一条无向边。设 $L(i,j)$ 表示结点 $i$ 和 $j$ 最早在第 $L(i,j)$ 次操作后连通。 在 $m$ 次操作完后，你要求出 $\sum_{i=1}^n\sum_{j=i+1}^nL(i,j)$ 的值。 思路：这是基础并查集的应用，并查集记录一下子树的大小。考虑统计每次操作的贡献。如果第 $i$ 次操作 $a_i$ 和 $b_i$ 分属于两个不同子树，就将这两个子树合并，并将两者子树大小的乘积乘上 i 累加到答案里。时间复杂度 $O(n\alpha(n))$。 @@ ### $B$ 有 $n$ 个点，初始时均为孤立点。 接下来有 $m$ 次加边操作，第 $i$ 次操作在 $a_i$ 和 $b_i$ 之间加一条无向边。 接下来有 $q$ 次询问，第 $i$ 次询问 $u_i$ 和 $v_i$ 最早在第几次操作后连通。 思路：考虑在并查集合并的时候记录「并查集生成树」，也就是说如果第 $i$ 次操作 $a_i$ 和 $b_i$ 分属于两个不同子树，那么把 $(a_i,b_i)$ 这条边纳入生成树中。边权是 $i$。那么查询就是询问 $u$ 到 $v$ 路径上边权的最大值，可以使用树上倍增或者树链剖分的方法维护。时间复杂度 $O(n\log n)$。 另外一个方法是维护 $\text{Kruskal}$ 重构树，其本质与并查集生成树是相同的。复杂度亦相同。 @@ ### $C$ 有 $n$ 个点，初始时均为孤立点。 接下来有 $m$ 次加边操作，第 $i$ 次操作在 $a_i$ 和 $b_i$ 之间加一条无向边。 接下来有 $q$ 次询问，第 $i$ 次询问第 $x_i$ 个点在第 $t_i$ 次操作后所在连通块的大小。 @@ 离线算法：考虑将询问按 $t_i$ 从小到大排序。在加边的过程中使用并查集顺便处理询问即可。时间复杂度 $O(q\log q+(n+q)\alpha(n))$。 在线算法：本题的在线算法只能使用 $\text{Kruskal}$ 重构树。$\text{Kruskal}$ 重构树与并查集的区别是：第 $i$ 次操作 $a_i$ 和 $b_i$ 分属于两个不同子树，那么 $\text{Kruskal}$ 会新建一个结点 $u$，然后让 $a_i$ 所在子树的根和 $b_i$ 所在子树的根分别连向 $u$，作为 $u$ 的两个儿子。不妨设 $u$ 的点权是 $i$。对于初始的 $n$ 个点，点权为 $0$。 对于询问，我们只需要求出 $x_i$ 在重构树中最大的一个连通块使得连通中的点权最大值不超过 $t_i$，询问的答案就是这个连通块中点权为 $0$ 的结点个数，即叶子结点个数。 由于我们操作的编号是递增的，因此重构树上父结点的点权总是大于子结点的点权。这意味着我们可以在重构树上从 $x_i$ 到根结点的路径上倍增找到点权最大的不超过 $t_i$ 的结点。这样我们就求出了答案。时间复杂度 $O(n\log n)$。 @@ ### $D$ 给一个长度为 $n$ 的 $01$ 序列 $a_1,\ldots,a_n$，一开始全是 $0$，接下来进行 $m$ 次操作： - 令 $a_x=1$； - 求 $a_x,a_{x+1},\ldots,a_n$ 中左数第一个为 $0$ 的位置。 思路：建立一个并查集，$f_i$ 表示 $a_i,a_{i+1},\ldots,a_n$ 中第一个 $0$ 的位置。初始时 $f_i=i$。 对于一次 $a_x=1$ 的操作，如果 $a_x$ 原本就等于 $1$，就不管。否则我们令 $f_x=f_{x+1}$。 时间复杂度 $O(n\log n)$，如果要使用按秩合并的话实现会较为麻烦，不过仍然可行。也就是说时间复杂度或为 $O(n\alpha(n))$。 @@ ### $E$ 给出三个长度为 $n$ 的正整数序列 $a$，$b$，$c$。枚举 $1\le i\le j\le n$，求 $a_i\cdot b_j\cdot \min_{i\le k\le j}c_k$ 的最大值。 思路：本题同样有许多做法，这里我们重点讲解并查集思路。按权值从大到小考虑 $c_k$。相当于我们在 $k$ 上加入一个点，然后将 $k-1$ 和 $k+1$ 位置上的点所在的连通块与之合并（如果这两个位置上有点的话）。连通块上记录 $a$ 的最大值和 $b$ 的最大值，即可在合并的时候更新答案。时间复杂度 $O(n\log n)$。 @@ ### $F$ 给出一棵 $n$ 个点的树，接下来有 $m$ 次操作： - 加一条从 $a_i$ 到 $b_i$ 的边。 - 询问两个点 $u_i$ 和 $v_i$ 之间是否有至少两条边不相交的路径。 思路：询问可以转化为：求 $u_i$ 和 $v_i$ 是否在同一个简单环上。按照双连通分量缩点的想法，每次我们在 $a_i$ 和 $b_i$ 间加一条边，就可以把 $a_i$ 到 $b_i$ 树上路径的点缩到一起。如果两条边 $(a_i,b_i)$ 和 $(a_j,b_j)$ 对应的树上路径有交，那么这两条边就会被缩到一起。 @@ 换言之，加边操作可以理解为，将 $a_i$ 到 $b_i$ 树上路径的边覆盖一次。而询问就转化为了：判断 $u_i$ 到 $v_i$ 路径上是否存在未被覆盖的边。如果不存在，那么 $u_i$ 和 $v_i$ 就属于同一个双连通分量，也就属于同一个简单环。 考虑使用并查集维护。给树定根，设 $f_i$ 表示 $i$ 到根的路径中第一个未被覆盖的边。那么每次加边操作，我们就暴力跳并查集。覆盖了一条边后，将这条边对应结点的 $f$ 与父节点合并。这样，每条边至多被覆盖一次，总复杂度 $O(n\log n)$。使用按秩合并的并查集同样可以做到 $O(n\alpha(n))$。 本题的维护方式类似于 D 的树上版本。 @@ ### $G$ 无向图 $G$ 有 $n$ 个点，初始时均为孤立点（即没有边）。 接下来有 $m$ 次加边操作，第 $i$ 次操作在 $a_i$ 和 $b_i$ 之间加一条无向边。 每次操作后，你均需要求出图中桥的个数。 桥的定义为：对于一条 $G$ 中的边 $(x,y)$，如果删掉它会使得连通块数量增加，则 $(x,y)$ 被称作桥。 强制在线。 思路：本题考察对并查集性质的理解。考虑用并查集维护连通情况。对于边双树，考虑维护有根树，设 $p_i$ 表示结点 $i$ 的父亲。也就是不带路径压缩的并查集。 @@ 如果第 $i$ 次操作 $a_i$ 和 $b_i$ 属于同一个连通块，那么我们就需要将边双树上 $a_i$ 到 $b_i$ 路径上的点缩起来。这可以用并查集维护。每次缩点，边双连通分量的个数减少 $1$，最多减少 $n-1$ 次，因此缩点部分的并查集复杂度是 $O(n\alpha(n))$。 为了缩点，我们要先求出 $a_i$ 和 $b_i$ 在边双树上的 $\text{LCA}$。对此我们可以维护一个标记数组。然后从 $a_i$ 和 $b_i$ 开始轮流沿着祖先一个一个往上跳，并标记沿途经过的点。一但跳到了某个之前就被标记过的点，那么这个点就是 $a_i$ 和 $b_i$ 的 $\text{LCA}$。这个算法的复杂度与 $a_i$ 到 $b_i$ 的路径长度是线性相关的，可以接受。 如果 $a_i$ 和 $b_i$ 分属于两个不同连通块，那么我们将这两个连通块合并，并且桥的数量加 $1$。此时我们需要将两个点所在的边双树连起来，也就是加一条 $a_i$ 到 $b_i$ 的边。因此我们需要将其中一棵树重新定根，然后接到另一棵树上。这里运用启发式合并的思想：我们把结点数更小的重新定根。这样的总复杂度是 $O(n\log n)$ 的。 综上，该算法的总复杂度是 $O(n\log n+m\log n)$ 的。 @@ ## 小结 并查集与 $\text{Kruskal}$ 重构树有许多共通点，而并查集的优化（按秩合并）正是启发式合并思想的应用。因此灵活运用并查集可以方便地处理许多与连通性有关的图论问题。